Other algorithms

I enjoy working on all kinds of algorithms.

Parallel shortest paths

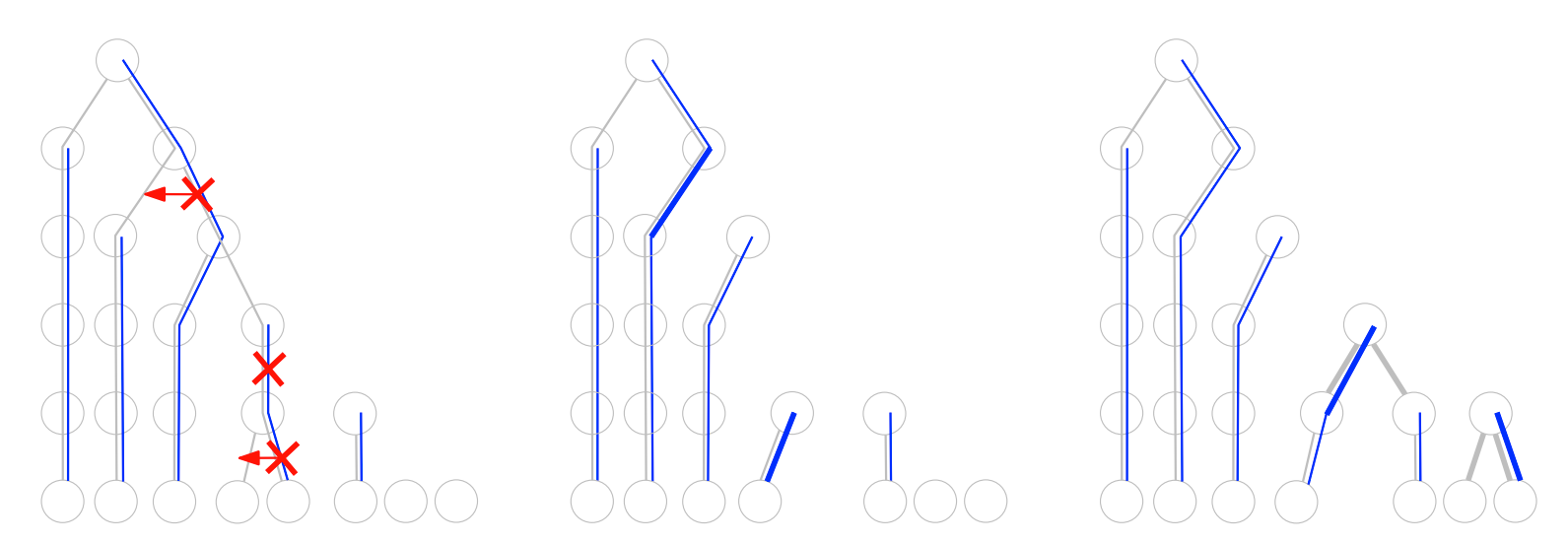
Dijkstra’s algorithm is a very efficient solution for the problem of finding the shortest path in a graph. But this algorithm is very sequential, so is there also an efficient parallel algorithm for this problem? For a long time, there was no known shortest-path algorithm that would keep reasonable (near-linear) total work and had nontrivial (truly sublinear) depth. In a paper with Christoph Grunau, Bernhard Haeupler, Anders Martinsson, Goran Zuzic, we showed that there is really an algorithm with near-linear work and about \(\sqrt{n}\) depth by reducing the problem to the approximate variant where an algorithm was already known.

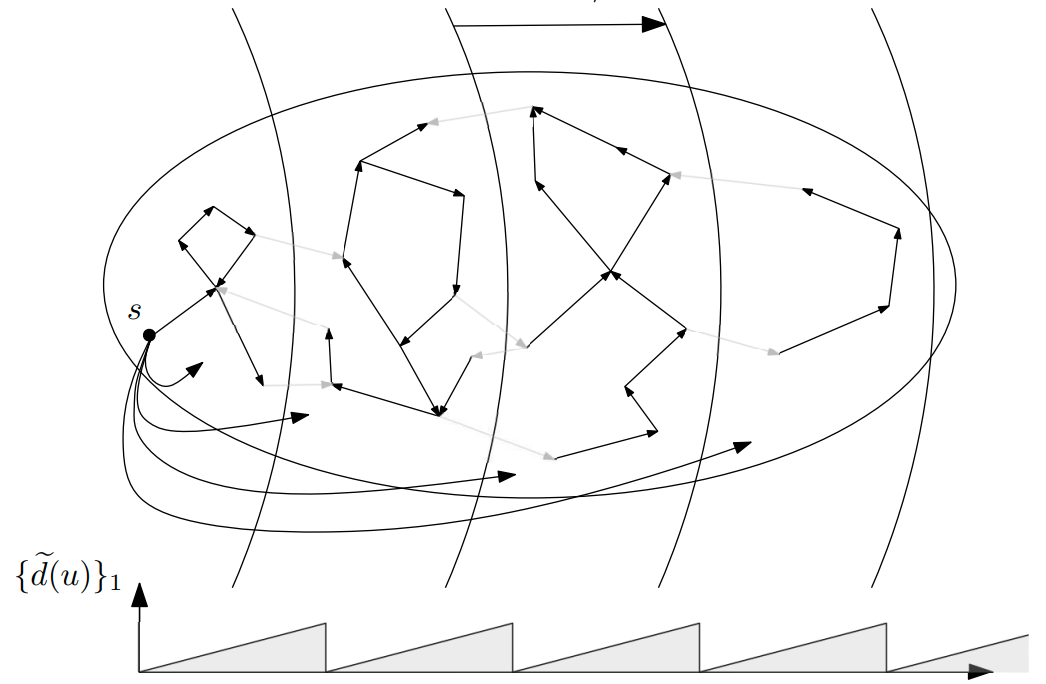
In other two papers with Christoph Grunau, Bernhard Haeupler, Michael Elkin, Jason Li, and Goran Zuzic, we first showed that on undirected graphs an 1.01-approximate shortest paths, we can get the ultimate solution: a deterministic near-linear-time and polylogarithmic-depth algorithm. Then, we showed how this can be used to solve a bunch of other problems with the same near-optimal guarantees. The upshot is that a lot of graph problems can be solved with algorithms that are near-optimal in terms of both their overall running time and parallelizability.

Parallel derandomization

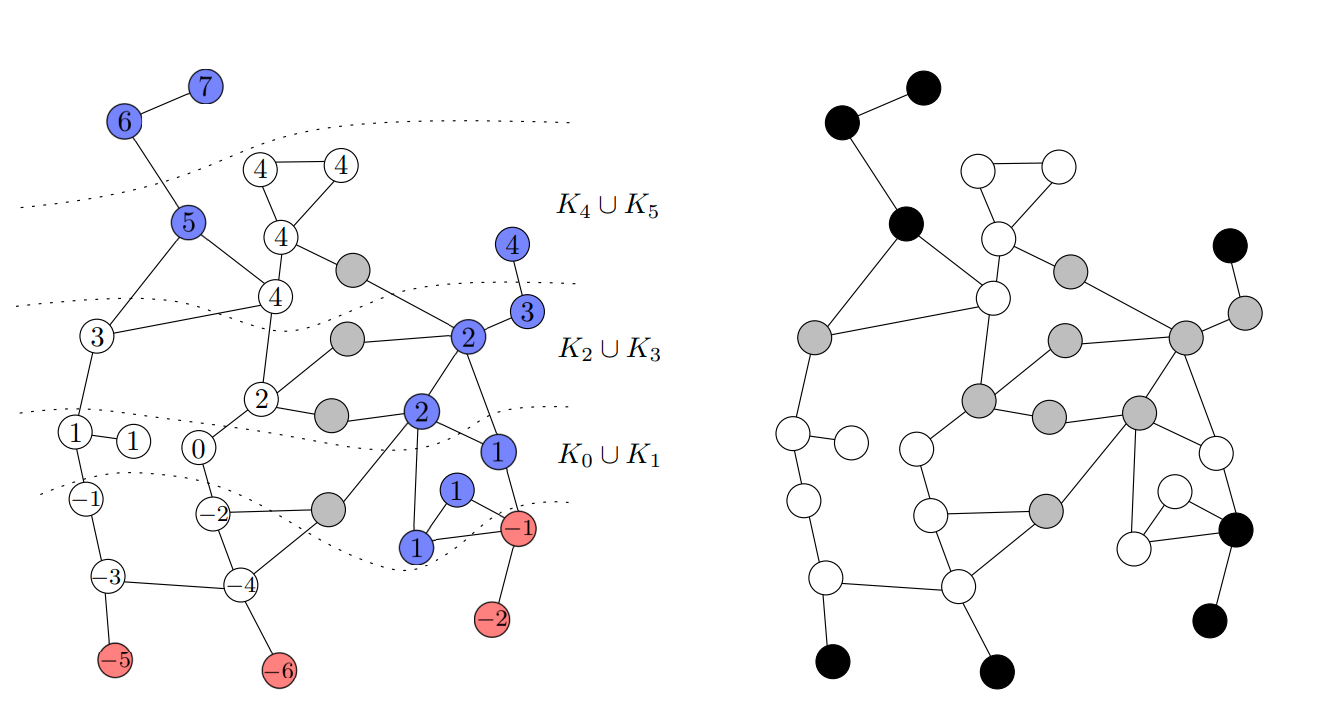
Here’s a big open computer science question: if there is a fast randomized algorithm for some problem, is there also a fast deterministic algorithm for it? Though we don’t know the answer, we have a bunch of quite general techniques, like the method of conditional expectations, to turn randomized algorithms into deterministic ones. In a paper with Mohsen Ghaffari and Christoph Grunau, we showed a quite general way of implementing this method in parallel; this makes it a bit more plausible that one can not only efficiently derandomize algorithms, but also keep their depth.

Consistent k-center

Let’s say that I want to compute some clustering on a set of points \(X\); to be concrete, let’s say I want to solve the k-center problem. The twist is that every day, \(X\) gets updated – either one new point arrives or one point from \(X\) gets removed. The field of dynamic algorithms is about solving the problem of quickly updating my solution every day.

But there’s an even more basic question to ask: after each update, is it possible to change only a few clusters and preserve that each day, my solution approximates the current optimum? This property is called consistency and in a paper with Christoph Grunau, Bernhard Haeupler, Rajesh Jarayam, and Jakub Lacki we showed that it is achievable for the k-center problem. In fact, swapping two centers each day suffices.