Local algorithms
Think of a huge network like the Internet. Each node in this network is a tiny computer that can only see its immediate neighborhood. Let’s say that in one round, each node can send any message to its neighbors, receive their messages, and run some algorithm on them. This is the model of local algorithms.
What kind of problems can and cannot be solved in this model? This is a question that many people have worked on since early 80’s, and we now have a pretty good understanding of it! It also seems that local algorithms are tightly related not only to distributed computing, but more generally to all kinds of parallel, sublinear, or dynamic algorithms and even fundamental questions in graph theory, probability, and measure theory.
I worked on a few aspects of local algorithms and also wrote an introductory text about them.
Introductory text
I wrote an introductory text / survey about local algorithms. It’s written for a younger version of myself, something that would hopefully bring me up to speed and made me able to understand papers in the area in a broader context.
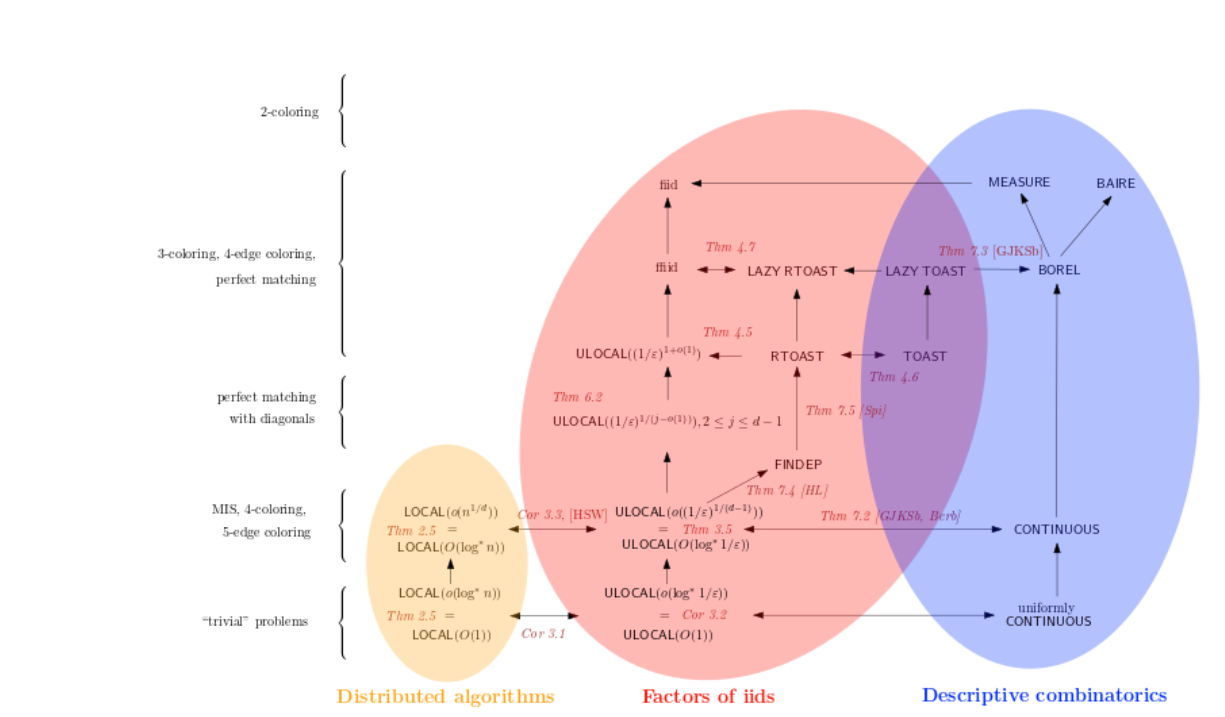
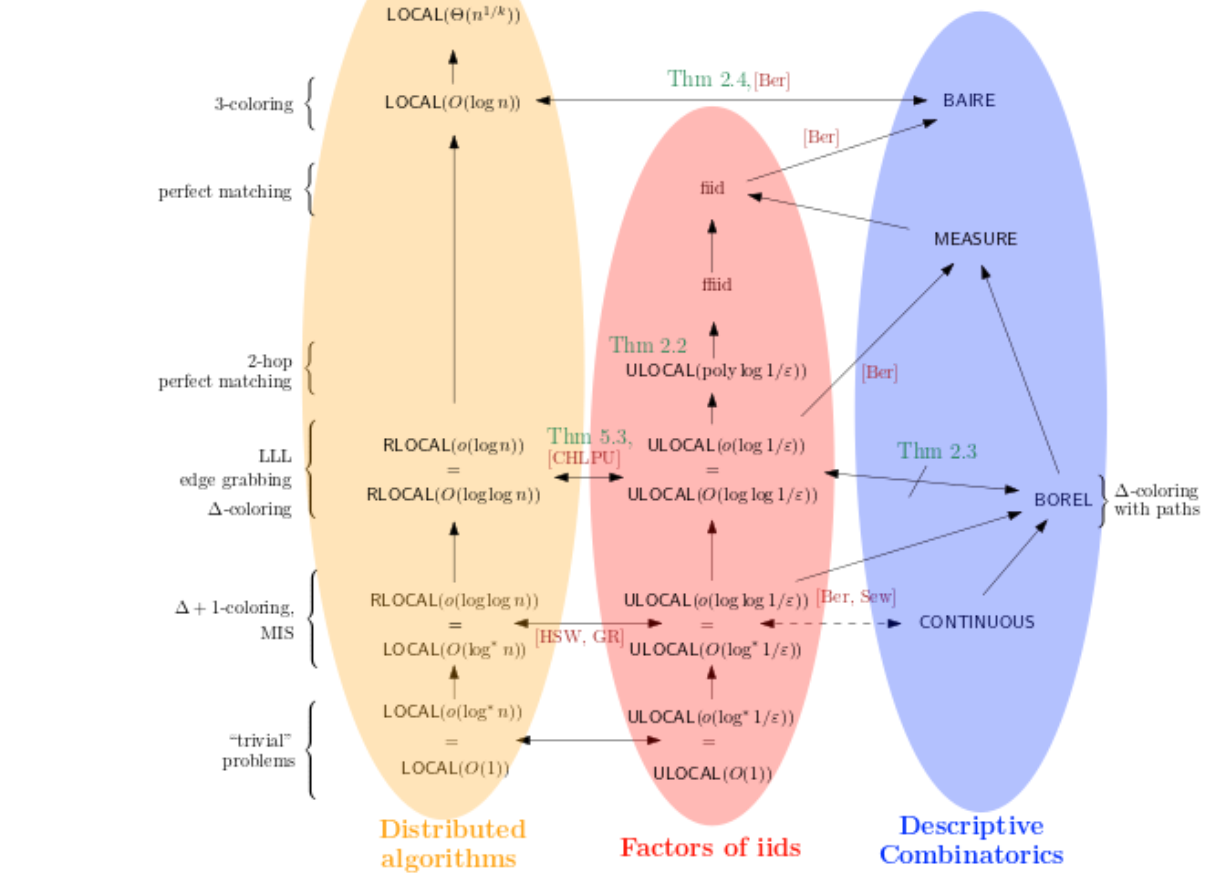
But also – local algorithms are one of the precious few areas of computer science that we can understand better than just by having a bunch of techniques, algorithms, and important open problems. In local algorithms, we have a theory! For example, one of the most important recently-proved theorems says that there are only four types of local problems, each type being interesting for different reasons. This theorem was proven over a few decades in a series of several papers that used and developed all kinds of different techniques. The introductory text is, as far as I can say, the only place that proves this particular theorems (and others) from scratch and in one place. Hopefully, this can help us to have a clearer picture of what’s going on.
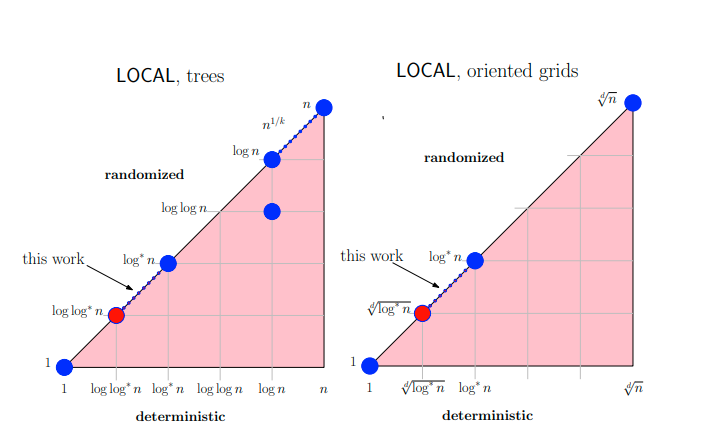
Network decomposition
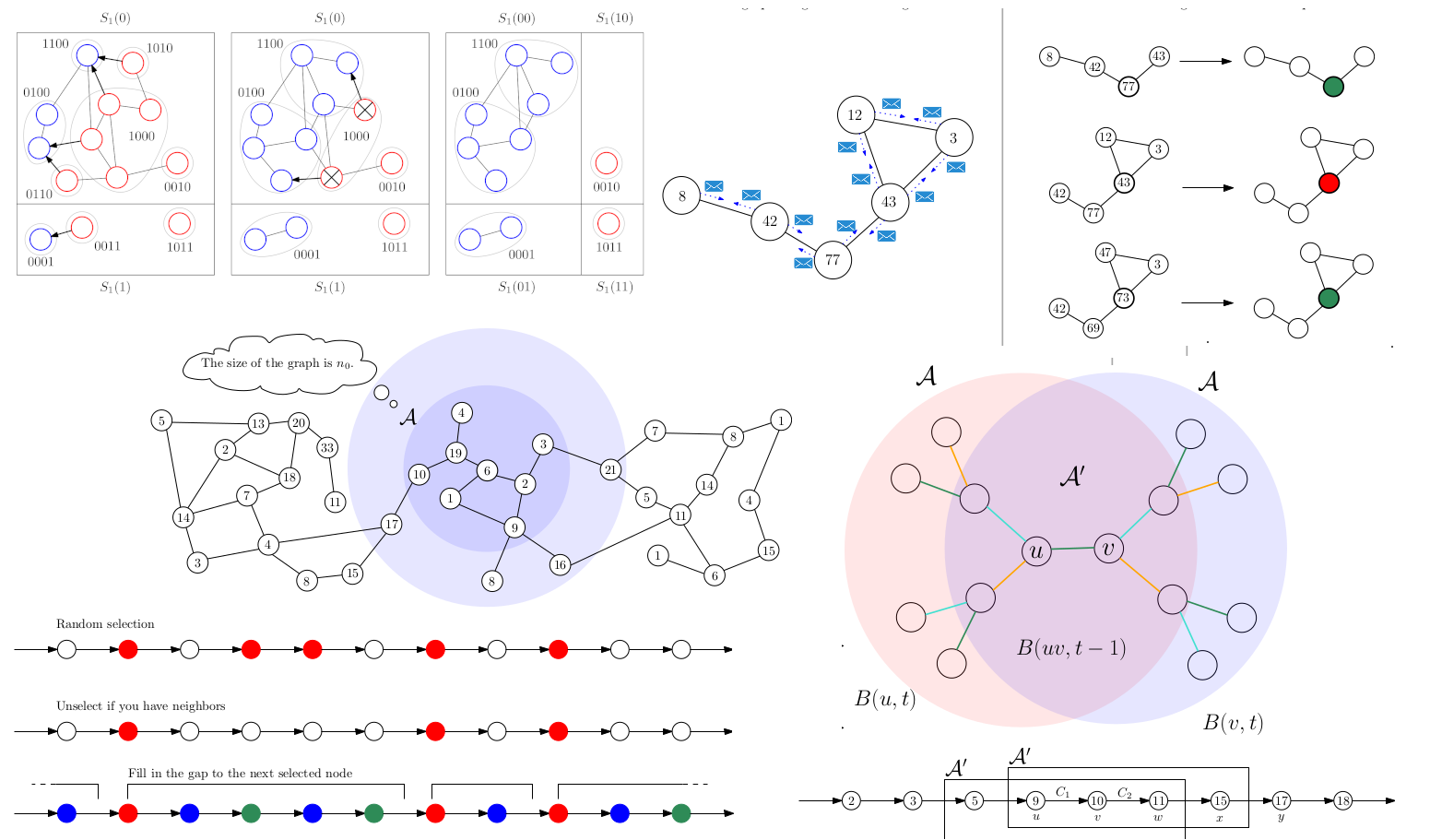
Network decomposition is a certain clustering problem that is extremely important for the understanding of local algorithms, especially if you want to understand what kind of problems can be solved in a reasonably efficient way (I explain this properly in the survey). In a paper with Mohsen Ghaffari, we constructed the first polylogarithmic deterministic algorithm for network decomposition. Subsequently, Christoph Grunau, Mohsen and others came up with a more principled way of solving the problem, which resulted in somewhat faster algorithms, potentially culminating with this one.
Classification theorems
In some cases, we understand local algorithms so well that we can prove so-called classification theorems. Those theorems basically prove that each reasonable problem can have only one of a few possible complexities. Such theorems are incredibly powerful – when we encounter a new problem, it suffices to find out which category it belongs to, and then the general theorem tells us what the complexity of that problem is! I explain some of these theorems in the survey.
With Christoph Grunau, Sebastian Brandt and others we have proved some small parts of these classification results in a few papers and extended them to some related models in a few papers.
Connections to other fields
An amazing paper of Anton Bernshteyn showed that local algorithms can directly imply results in the field of descriptive combinatorics that tries to understand uncountable objects equipped with measure. Together with Jan Grebík, we set out to connect the two fields, together with the model of finitary factors coming from probability theory. We used an abstract, complexity-theoretical approach that extends the classification theorems from the area of local algorithms (here’s some papers). It really seems that there is some kind of underlying theory, and we are in the process of revealing its facets.