Discrete math

I did some discrete math research in undergrad. Most of it is related to extremal graph theory – an area studying various parameters of graphs by asking questions like “If a graph has \(n\) vertices and \(m\) edges, what’s the minimal and maximum number of triangles it can have?” More concretely, I did some research on graph homomorphisms and tree embedding.

Alternative characterization of graph norms

Given a large graph, we might be interested in the density of triangles, four-cycles or, more generally, the density of some small graph \(H\) in it. However, not all small graphs \(H\) are created equal, only the density of some of them has nice mathematical properties.

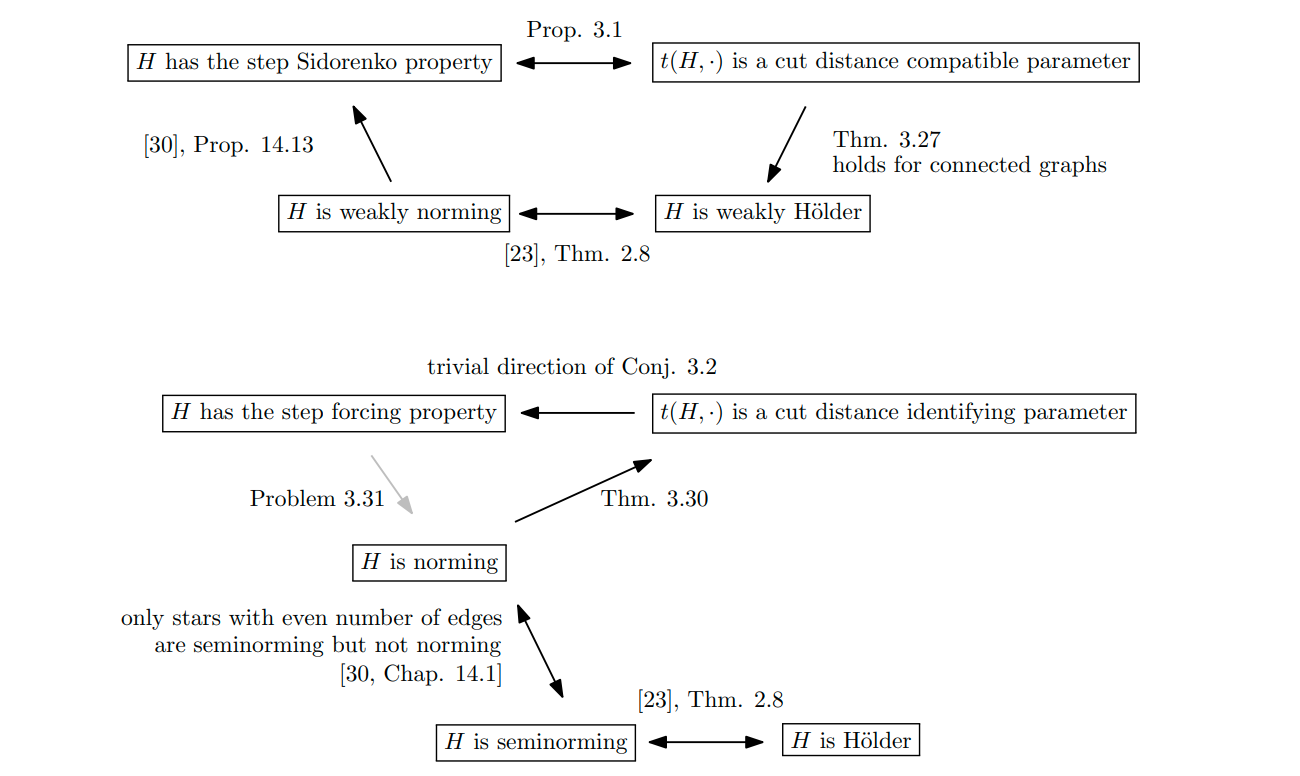
One of the most basic properties is that the density behaves as a norm – these graphs \(H\) are called weakly norming. A related property, called step Sidorenko property, roughly speaking says that if you make a large graph look more random, the density of \(H\) in it goes down or stays the same. In a paper with Martin Doležal, Jan Grebík, Jan Hladký, and Israel Rocha, we proved that these two properties are actually equivalent!

Graphs that contain every tree

In two papers with Tereza Klimošová and Diana Piguet, we studied what kind of graphs have the property that they contain all trees on \(k\) vertices as subgraphs. For example, there’s a famous Erdos-Sos conjecture that states that graphs of average degree at least \(k\) should have this property; a result in this paper of mine implied a weaker version of that conjecture.