Research
I have the full list of publications here or at Google Scholar. But I think that I can convey more information by briefly describing some selected projects I worked on. 1 In the following sections, each header/picture links to a separate page discussing the topic at greater length.
Local algorithms
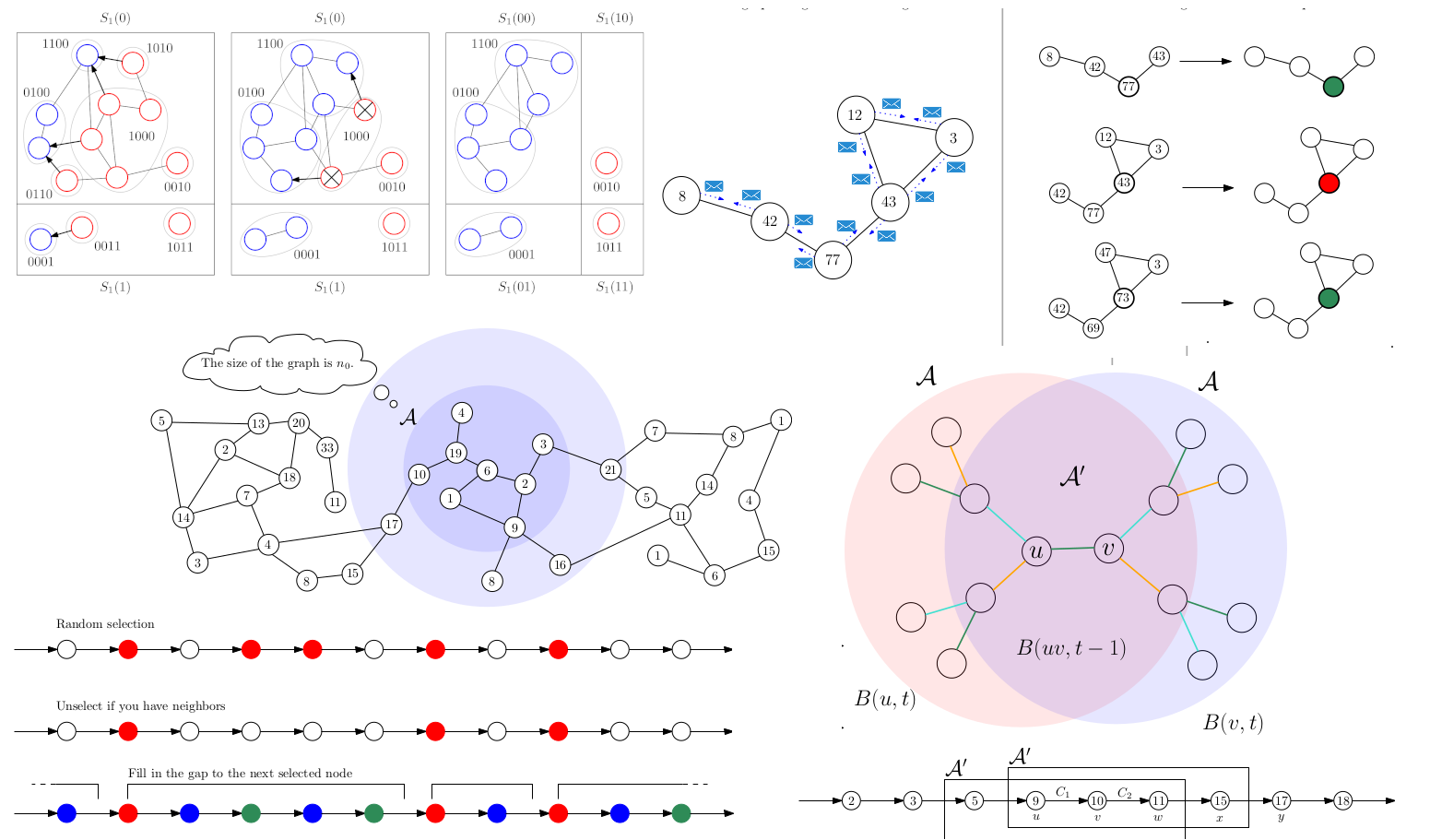
Local algorithms are a simplified model of algorithms that aims to underpin some fundamental principles of distributed, parallel, or sublinear algorithms. I am pretty certain that local algorithms will play a crucial role in whatever unifying theory of these algorithmic setups we end up having.
During my PhD, I worked a lot on local algorithms, both in terms of extending the theory behind them and linking it to other areas in computer science and mathematics. The necessity of writing some kind of thesis then motivated me to write an introductory text / survey about local algorithms. The text presents an overview of the field and is intended for students or researchers from adjacent areas.
Instance optimality
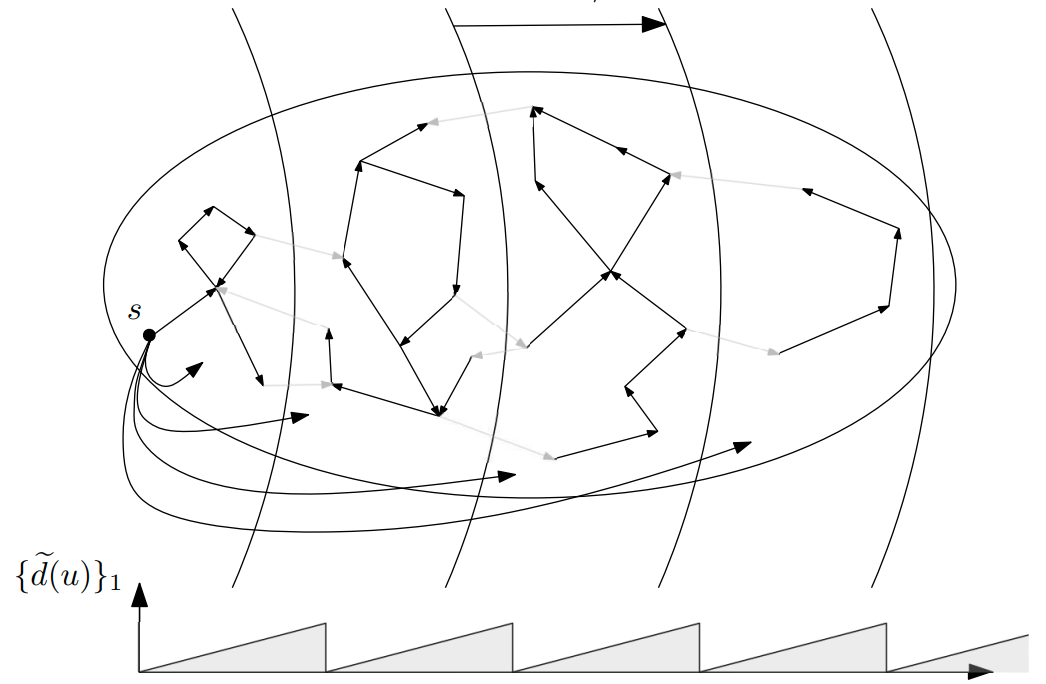
Instance optimality is pretty much the strongest guarantee that an algorithm can have; roughly speaking, it says that the algorithm is the best possible not only if you measure its complexity as the function of the input size (that would be the classical worst-case complexity), but it’s actually the best possible algorithm for every single input. This guarantee is so extremely strong that it’s also typically impossible to achieve it.
Yet, in some models of computation, like distributed algorithms, comparison-based algorithms, or sampling algorithms, instance optimality (or its cousins like universal optimality) are achievable! This makes those areas some kind of happy algorithmic places where we can almost dare to say that we understand what’s going on.
One of our instance-optimality results on Dijkstra’s algorithm won the FOCS best paper award and was featured in Quanta Magazine and Wired.
A picture from Quanta magazine.
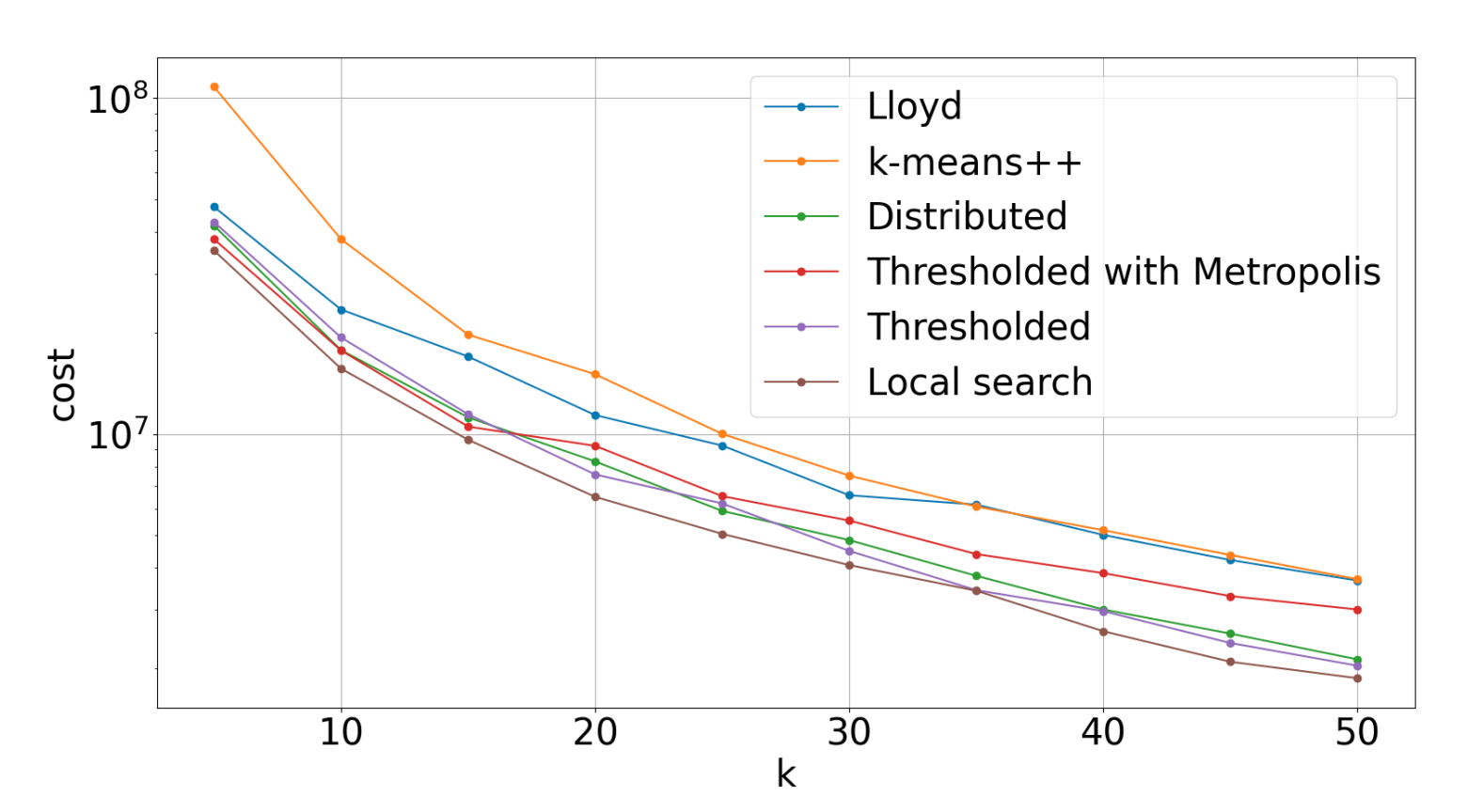
Practical k-means algorithms
Clustering is one of the most basic tasks in statistics or machine learning. And the most basic way of doing it is \(k\)-means. There is an enormous theoretical literature on the \(k\)-means problem, but the algorithms are mostly not practical. In a series of papers with Christoph Grunau and others, we analyzed the algorithms that are used in practice, and developed some new ones that seem to be practical.
For example, we proved that the \(k\)-means algorithm implemented in the Scikit-learn library always works! By that I mean that the solution returned by the algorithm can never be too far from optimal.
Various algorithms
I enjoy working on all kinds of algorithmic topics. This often means clustering or graph algorithms that are often parallel or distributed.
Discrete math
I did some discrete math research as an undergraduate. Most of it is related to extremal graph theory – an area studying various parameters of graphs by asking questions like “If a graph has \(n\) vertices and \(m\) edges, what’s the minimum and maximum number of triangles it can have?” More concretely, I did some research on graph homomorphisms and tree embedding.
-
More honestly, I am writing this after I’ve finished my PhD, trying to look back and wondering how to think of my research so far and what to focus on next. ↩